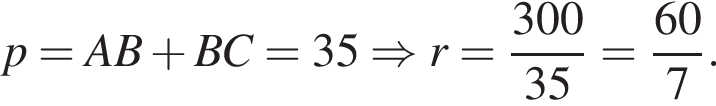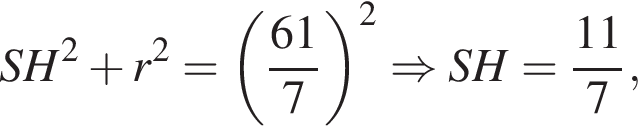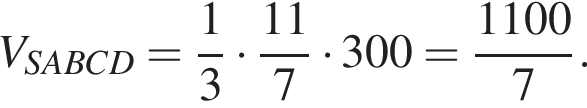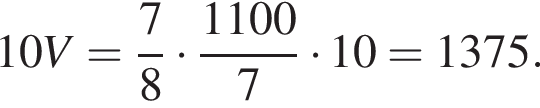Укажите номер точки, которая принадлежит графику функции y = 5x.
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.
Укажите номер выражения, которое определяет, сколько сантиметров в х м 9 дм.
| 1) 100х + 9; | 2) 100х + 90 | 3) 90x | 4) 10x + 90 | 5) 10x + 9 |
Даны квадратные уравнения:
Укажите уравнение, которое не имеет корней.
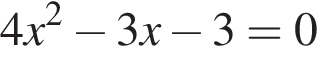
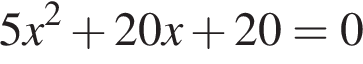
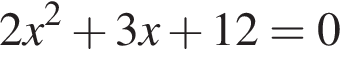
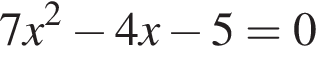
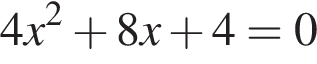
Точка С делит отрезок АВ в отношении 5 : 3, считая от точки А. Если длина отрезка АВ равна 24, то длина отрезка СВ равна:
Найдите значение выражения 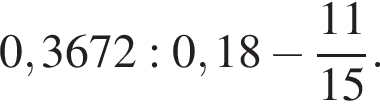
Сумма корней (или корень, если он один) уравнения 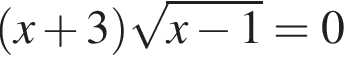 равна:
равна:
Среди данных утверждений укажите номер верного.
Ha координатной плоскости даны точки А и М, расположенные в узлах сетки (см. рис.). Укажите координаты точки, симметричной точке А относительно точки М.
Решением системы неравенств 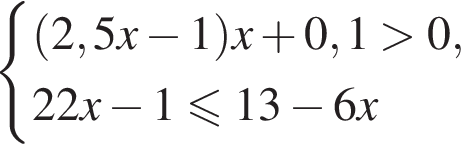 является:
является:
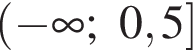
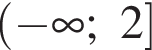


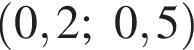
Укажите область значений функции
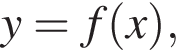 заданной графиком на промежутке [−2; 4] (см. рис.).
заданной графиком на промежутке [−2; 4] (см. рис.).
Укажите номер рисунка, на котором представлен эскиз графика функции y = 1 − (x + 3)2.
Найдите значение выражения 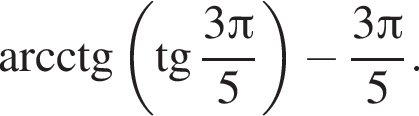
Основанием прямой треугольной призмы ABCA1B1C1 является треугольник АВС, в котором 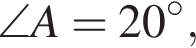
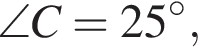 а радиус описанной около него окружности равен
а радиус описанной около него окружности равен ![]() Найдите длину диагонали грани AA1C1C, если площадь этой грани равна
Найдите длину диагонали грани AA1C1C, если площадь этой грани равна ![]()
Окружность задана уравнением 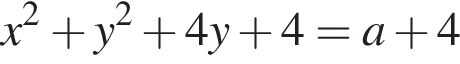 и проходит через вершину параболы
и проходит через вершину параболы 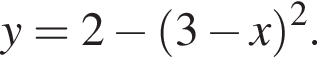 Найдите радиус этой окружности.
Найдите радиус этой окружности.
Какая из прямых пересекает график функции 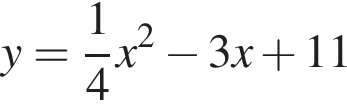 в двух точках?
в двух точках?
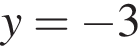


График функции, заданной формулой y = kx + b, симметричен относительно начала координат и проходит через точку A (2; 10). Значение выражения k + b равно:
Функции заданы формулами:
1) 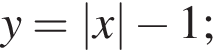 | 2) 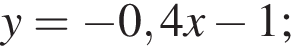 | 3) 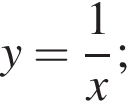 |
4) 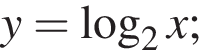 | 5) 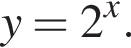 |
Выберите функцию, график которой имеет с графиком функции 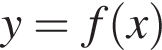 (см. рис.), заданной на промежутке [−5; 6], наибольшее количество точек пересечения.
(см. рис.), заданной на промежутке [−5; 6], наибольшее количество точек пересечения.

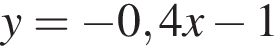
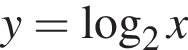
Витя купил в магазине некоторое количество тетрадей, заплатив за них 24 тысячи рублей. Затем он обнаружил, что в другом магазине тетрадь стоит на 1 тысячу рублей меньше, поэтому, заплатив такую же сумму, он мог бы купить на 2 тетради больше. Сколько тетрадей купил Витя?
Найдите сумму корней (корень, если он единственный) уравнения 
Известно, что при a, равном −2 и 4, значение выражения 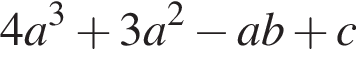 равно нулю. Найдите значение выражения b + с.
равно нулю. Найдите значение выражения b + с.
Пусть (x;y) — целочисленное решение системы уравнений
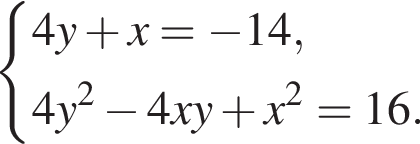
Найдите сумму x+y.
В параллелограмме с острым углом 45° точка пересения диагоналей удалена от прямых, содержащих неравные стороны, на расстояния ![]() и 2. Найдите площадь параллелограмма.
и 2. Найдите площадь параллелограмма.
Найдите сумму целых решений неравенства 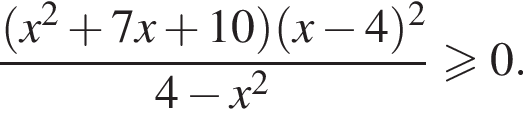
Решите уравнение 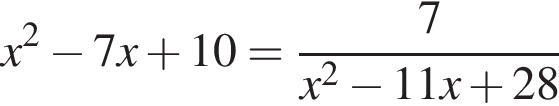 и найдите сумму его корней.
и найдите сумму его корней.
Найдите сумму наименьшего и наибольшего целых решений неравенства 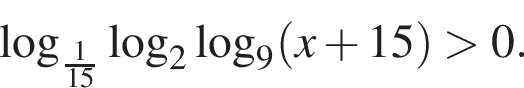
Найдите количество корней уравнения 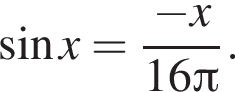
Из точки А проведены к окружности радиусом ![]() касательная AB (B — точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках D и C (AD < AC). Найдите площадь S треугольника ABC, если длина отрезка AC в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 5S.
касательная AB (B — точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках D и C (AD < AC). Найдите площадь S треугольника ABC, если длина отрезка AC в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 5S.
Из двух растворов с различным процентным содержанием спирта массой 100 г и 900 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
ABCA1В1С1 — правильная треугольная призма, у которой сторона основания и боковое ребро имеют длину 6. Через середины ребер АС и BB1 и вершину A1 призмы проведена секущая плоскость. Найдите площадь сечения призмы этой плоскостью.
Петя записал на доске два различных натуральных числа. Затем он их сложил, перемножил, вычел из большего записанного числа меньшее и разделил большее на меньшее. Сложив четыре полученных результата, Петя получил число 1521. Найдите все такие пары натуральных чисел. В ответ запишите их сумму.
Основанием пирамиды SABCD является выпуклый четырехугольник ABCD, диагонали АС и BD которого перпендикулярны и пересекаются в точке O, АО = 9, ОС = 16, ВО = OD = 12. Вершина S пирамиды SABCD удалена на расстояние ![]() от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.
от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.

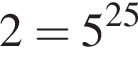 — неверно,
— неверно, — неверно,
— неверно, — неверно,
— неверно, — верно,
— верно,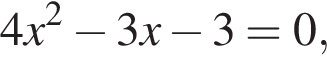 дискриминант больше нуля, значит, корни есть.
дискриминант больше нуля, значит, корни есть.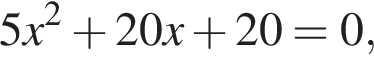 дискриминант равен нулю, значит, корень есть.
дискриминант равен нулю, значит, корень есть.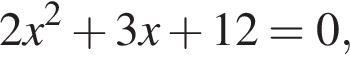 дискриминант меньше нуля, значит, корней нет.
дискриминант меньше нуля, значит, корней нет.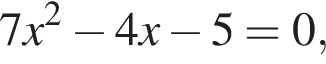 дискриминант больше нуля, значит, корни есть.
дискриминант больше нуля, значит, корни есть.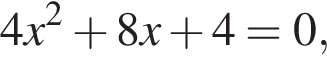 дискриминант равен нулю, значит, корень есть.
дискриминант равен нулю, значит, корень есть.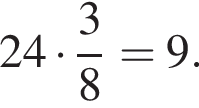
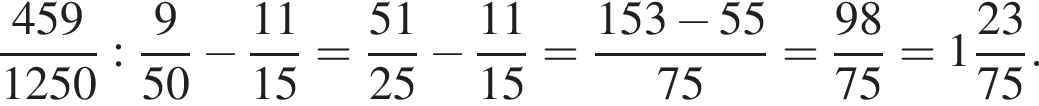
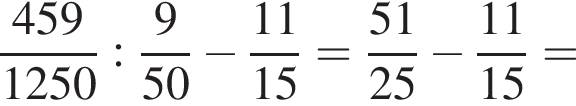
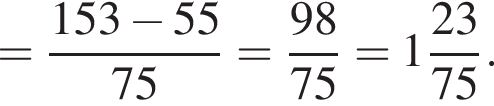
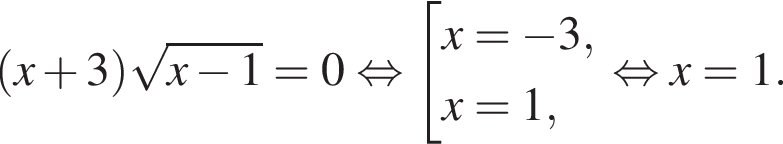
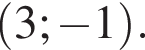
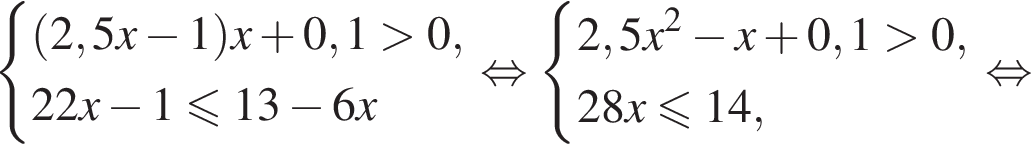
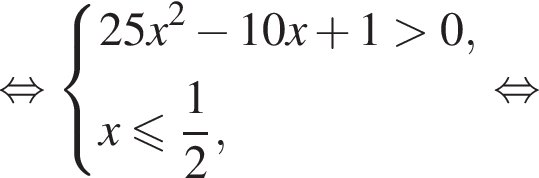
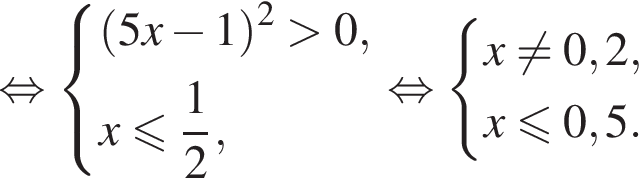
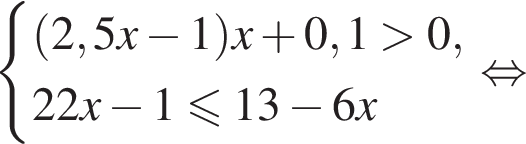
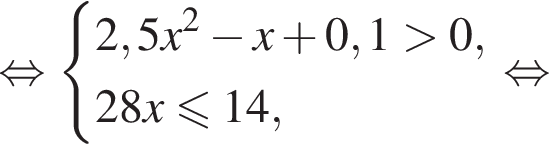
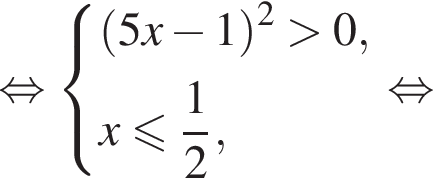
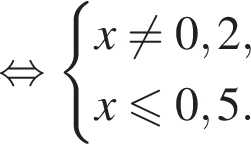
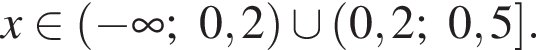
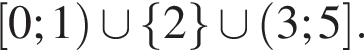
 только для
только для  Поэтому преобразуем, используя формулы приведения:
Поэтому преобразуем, используя формулы приведения: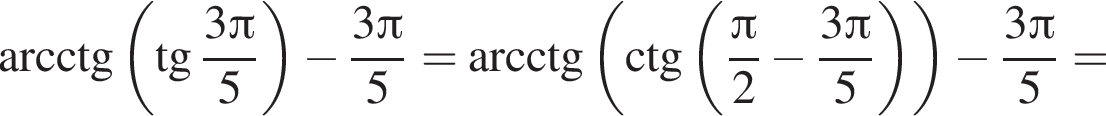
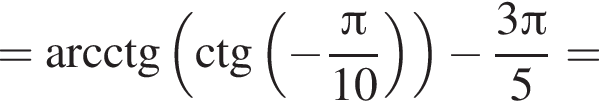
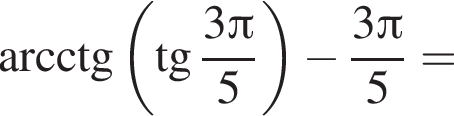
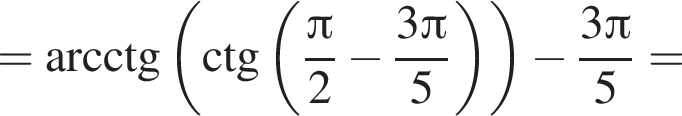
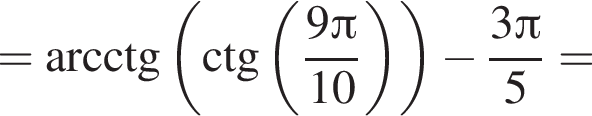
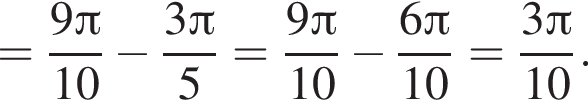
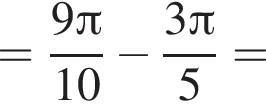
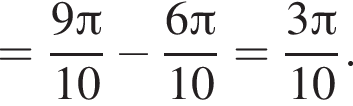
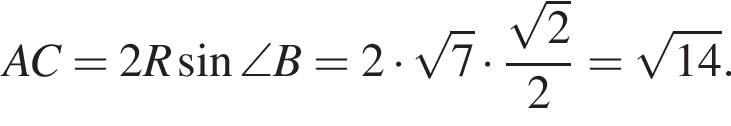
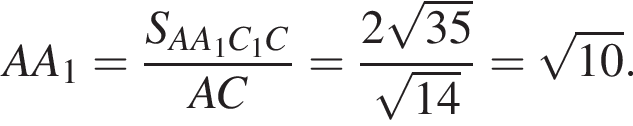
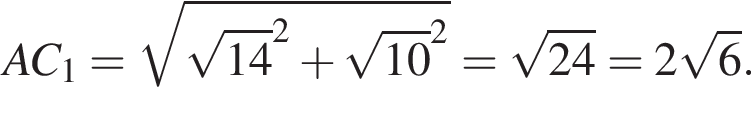
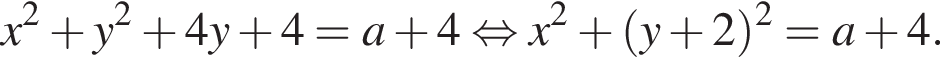
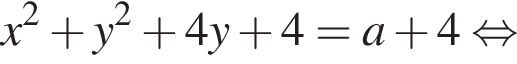
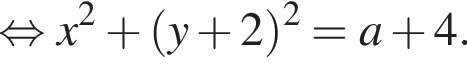
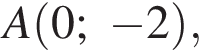 а радиус — это расстояние от точки A до вершины параболы.
а радиус — это расстояние от точки A до вершины параболы.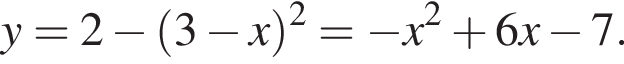
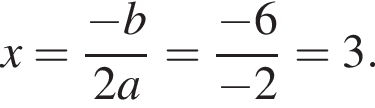 Подставим найденное значение x в изначальное уравнение параболы и получим
Подставим найденное значение x в изначальное уравнение параболы и получим 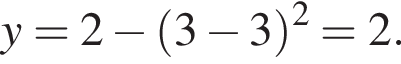 Таким образом, вершина параболы расположена в точке (3; 2).
Таким образом, вершина параболы расположена в точке (3; 2).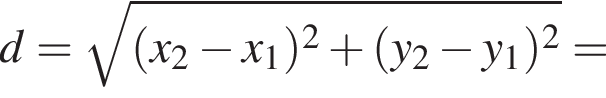
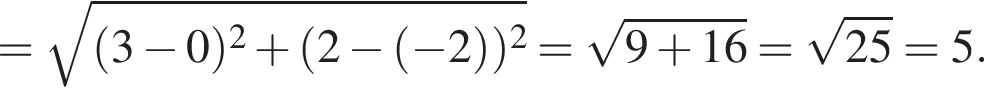
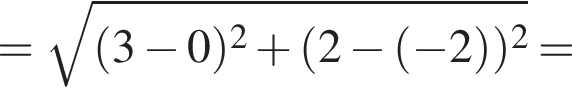
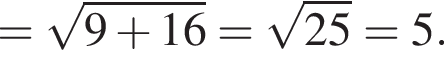
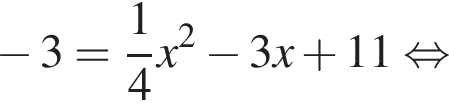
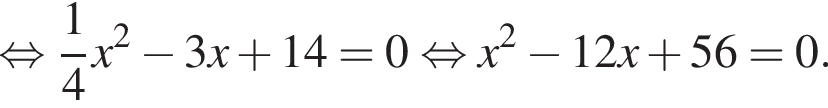
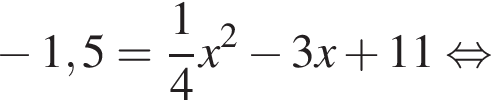
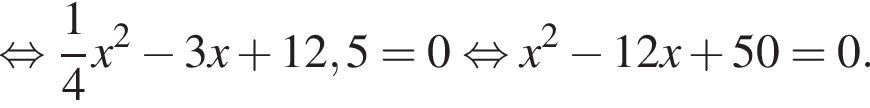
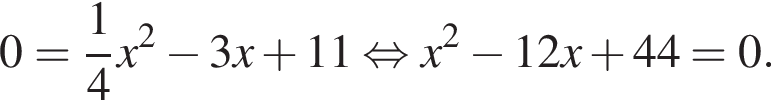 Дискриминант меньше нуля, поэтому пересечений нет.
Дискриминант меньше нуля, поэтому пересечений нет.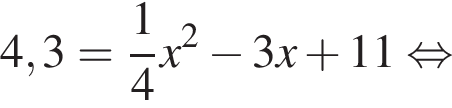
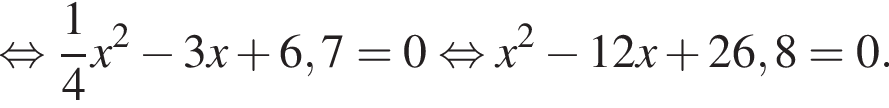
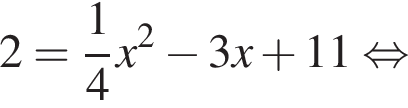
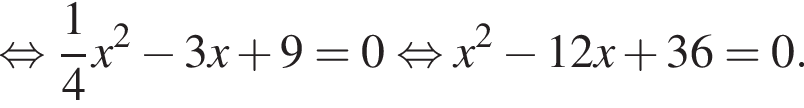
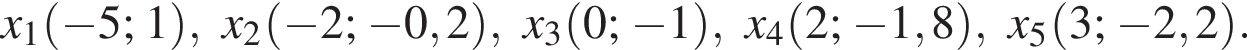
 Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство
Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство 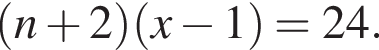 Решим систему уравнений:
Решим систему уравнений: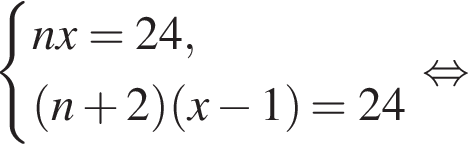
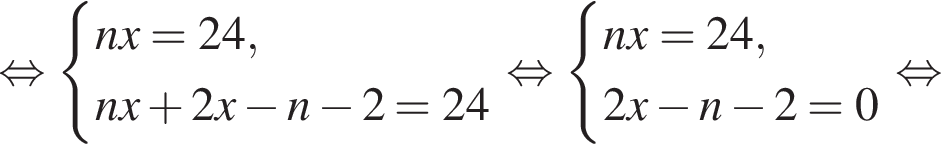
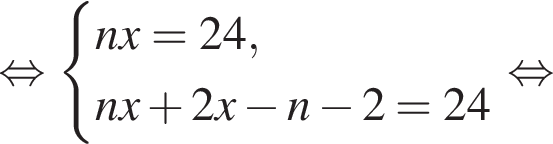
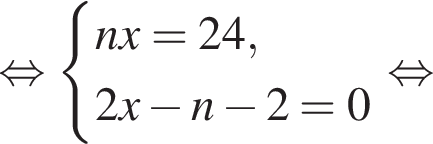
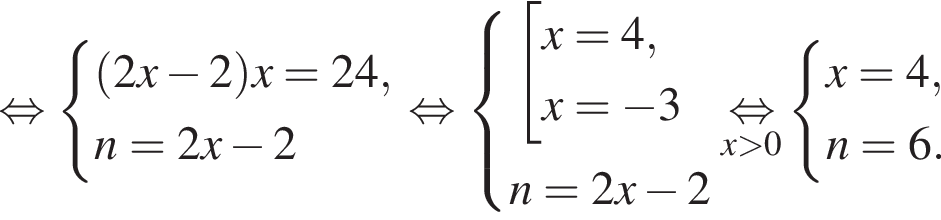
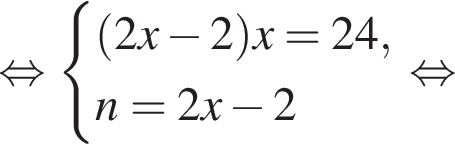
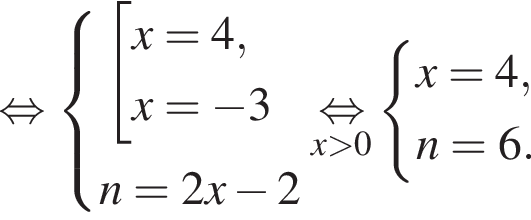
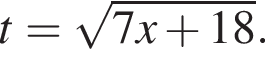 Тогда:
Тогда: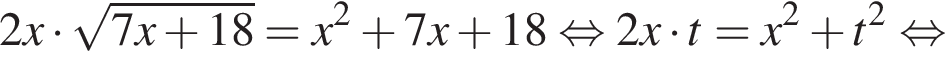

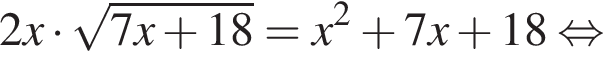


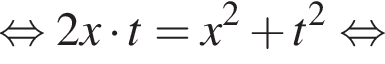
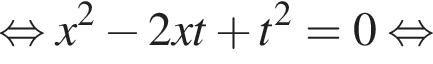
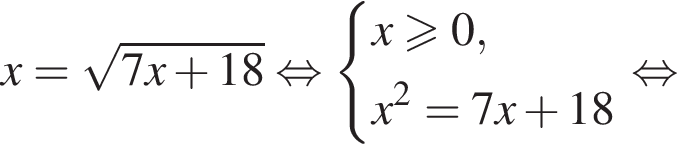
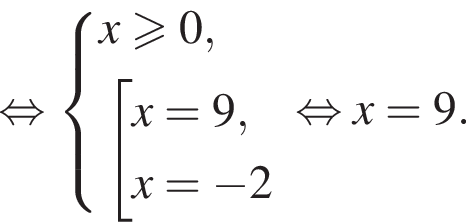
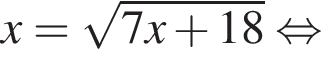
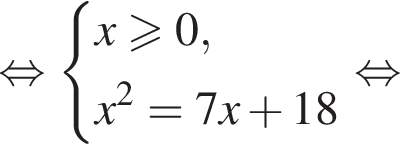
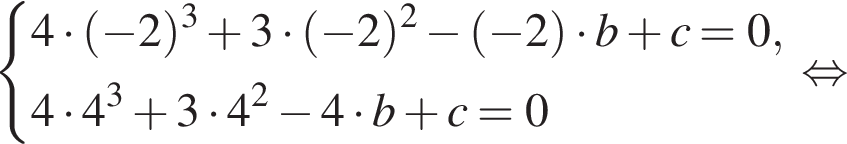
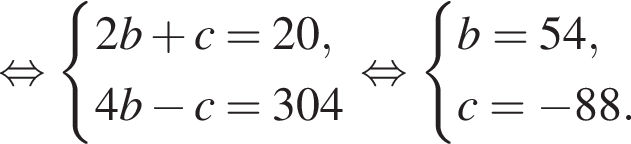
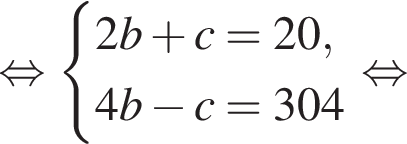
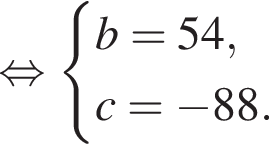

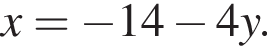 Заметим, что
Заметим, что 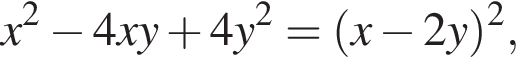 поэтому, подставляя x во второе уравнение системы получим:
поэтому, подставляя x во второе уравнение системы получим: 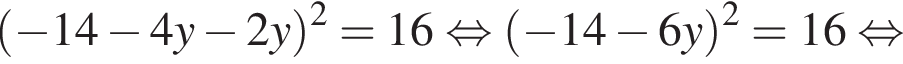
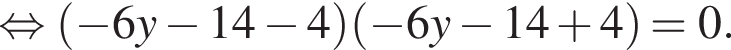
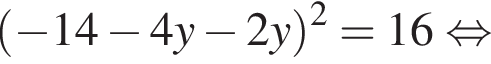
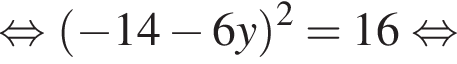
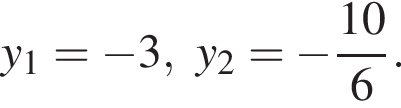 Поскольку по условию задачи требуются целочисленные решения системы, тогда найдем x:
Поскольку по условию задачи требуются целочисленные решения системы, тогда найдем x: 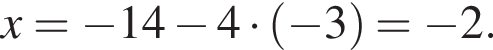 Сумма x+y равна:
Сумма x+y равна: 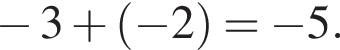
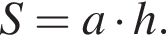 Синус известного угла есть отношение высоты и одной из сторон. Найдем одну из сторон параллелограмма, полагая, что высота равна 2 · 2 = 4:
Синус известного угла есть отношение высоты и одной из сторон. Найдем одну из сторон параллелограмма, полагая, что высота равна 2 · 2 = 4: 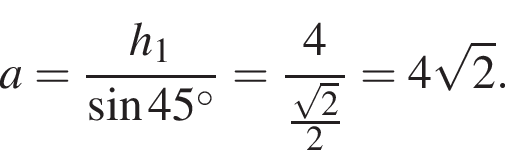 Таким образом, искомая площадь параллелограмма равна произведению найденной стороны на высоту
Таким образом, искомая площадь параллелограмма равна произведению найденной стороны на высоту 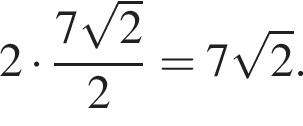
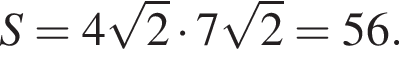
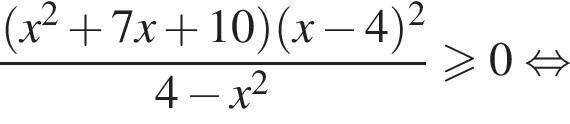
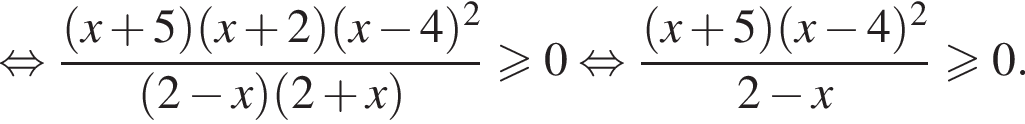
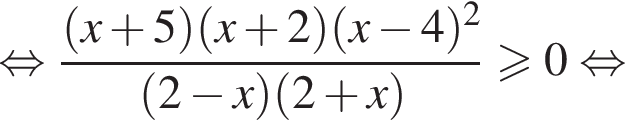
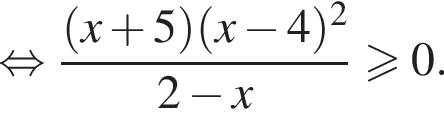
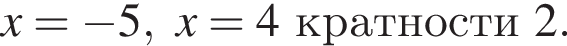 Корень знаменателя:
Корень знаменателя: 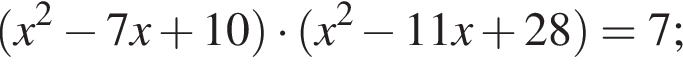
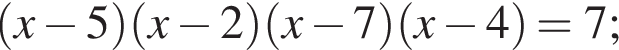
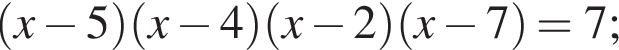
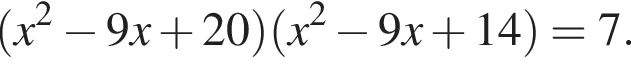
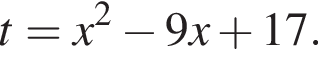 Получим:
Получим: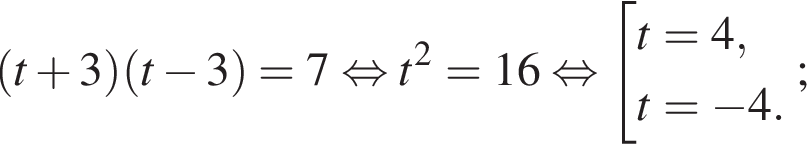
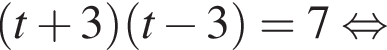
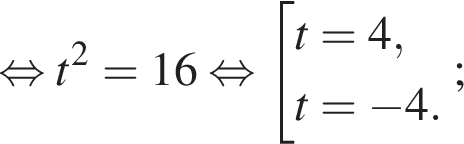
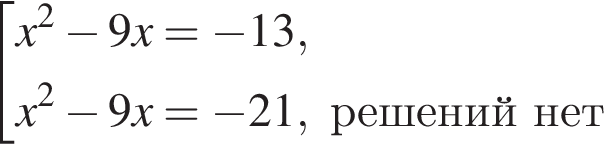
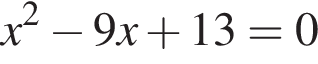 найдем по теореме Виета, она равна 9.
найдем по теореме Виета, она равна 9. искать ОДЗ не требуется.
искать ОДЗ не требуется.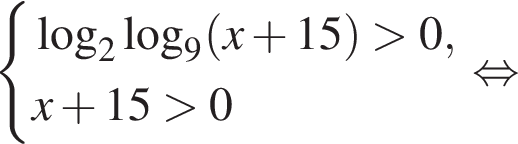
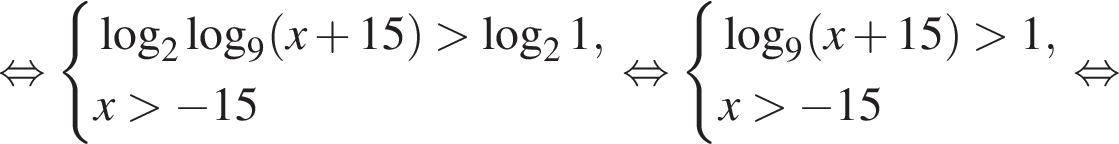
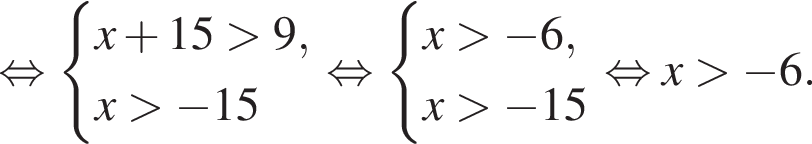
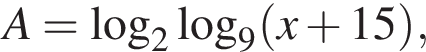 тогда:
тогда: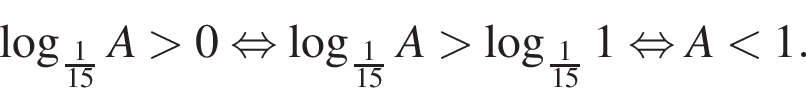
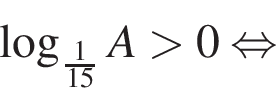
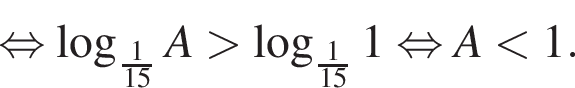

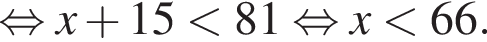


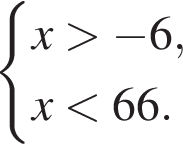 Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.
Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.
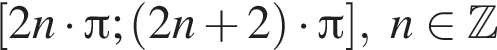 вплоть до
вплоть до 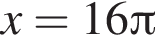 решений нет. Поэтому на положительной полуоси уравнение имеет 16 решений. На отрицательной полуоси будет столько же решений. Итого имеем 33 решения.
решений нет. Поэтому на положительной полуоси уравнение имеет 16 решений. На отрицательной полуоси будет столько же решений. Итого имеем 33 решения.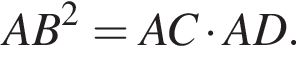 Обозначим AB за x, тогда
Обозначим AB за x, тогда  Тогда:
Тогда: 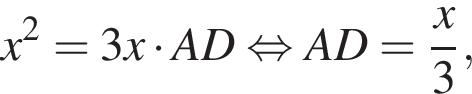 при этом
при этом 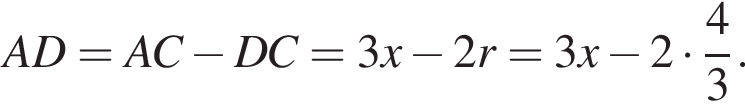 Получим:
Получим: 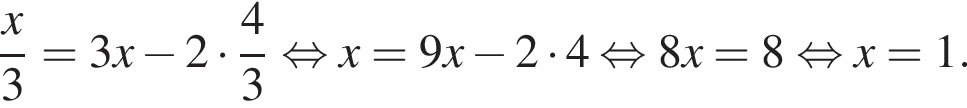
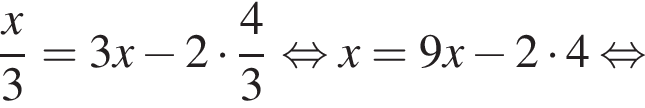
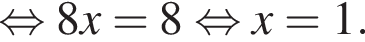
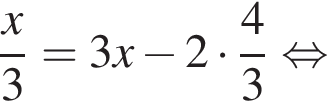
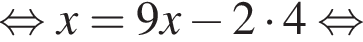
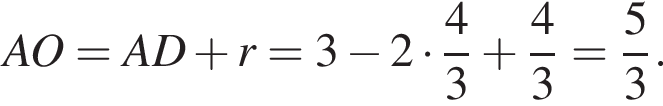
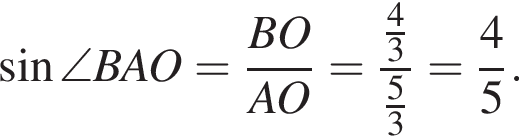 Тогда площадь треугольника ABC:
Тогда площадь треугольника ABC: 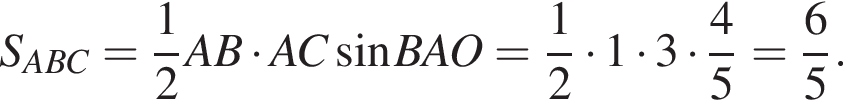
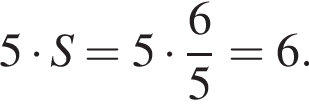
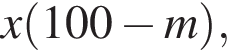 во втором —
во втором — 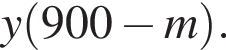 После переливания масса спирта в 1-ом сосуде равна
После переливания масса спирта в 1-ом сосуде равна 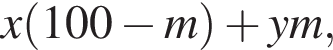 во втором —
во втором —  Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда:
Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда: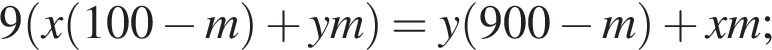
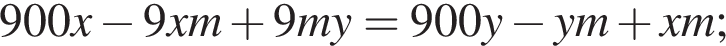

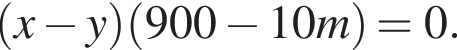

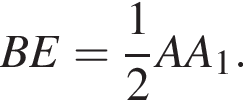 Отрезки CB и NM есть медианы треугольника ACN, поэтому CK : KB = 2 : 1, то есть CK = 4, BK = 2.
Отрезки CB и NM есть медианы треугольника ACN, поэтому CK : KB = 2 : 1, то есть CK = 4, BK = 2.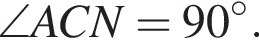 Тогда
Тогда 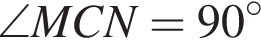 и
и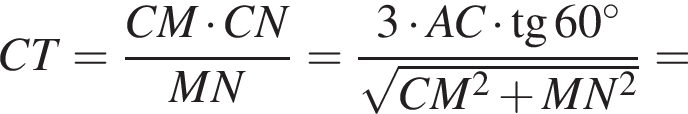
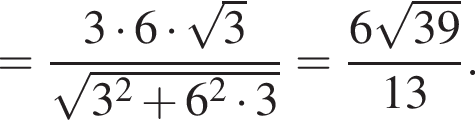
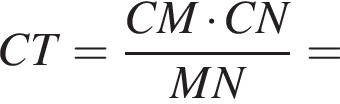
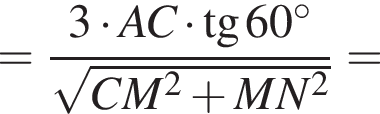
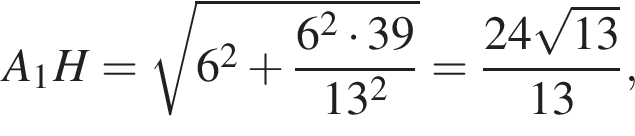
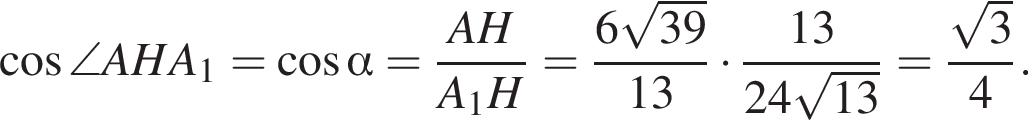
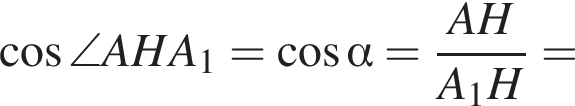
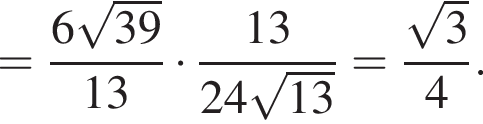

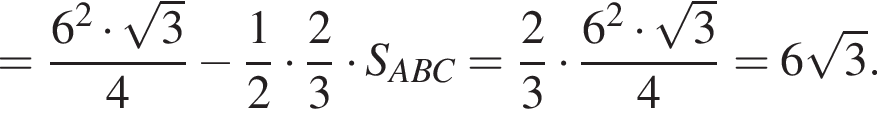
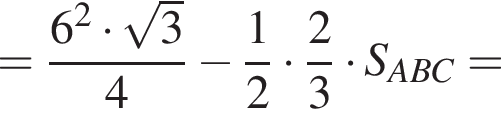
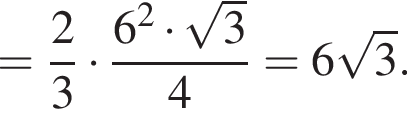
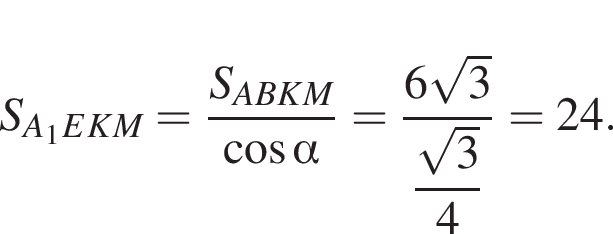
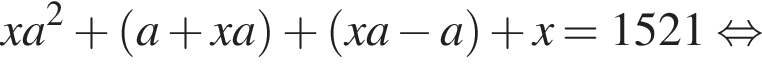
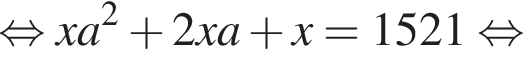

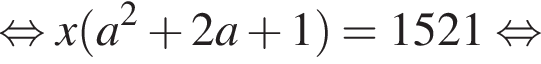
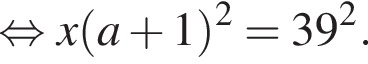
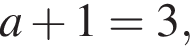
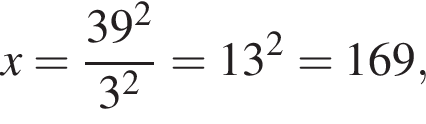
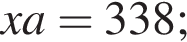
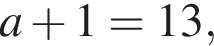
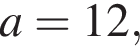
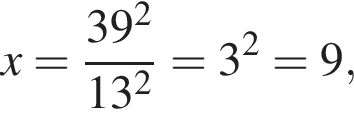
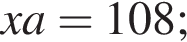
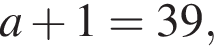
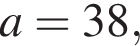
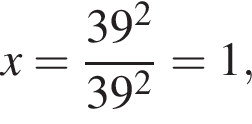
 что запрещено по условию.
что запрещено по условию.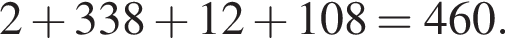
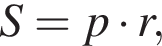 где p — полупериметр. Находим:
где p — полупериметр. Находим: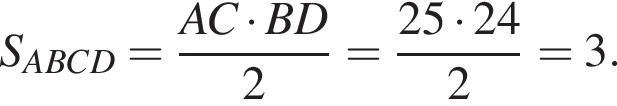
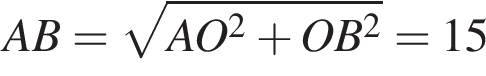 и
и 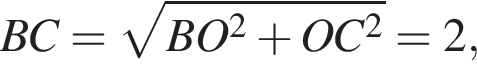 следовательно,
следовательно,